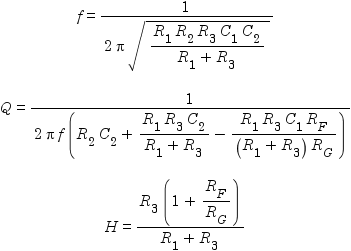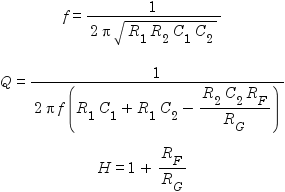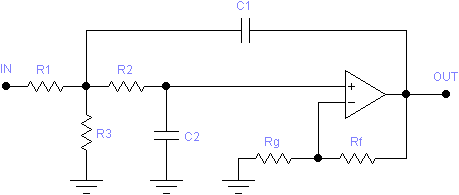
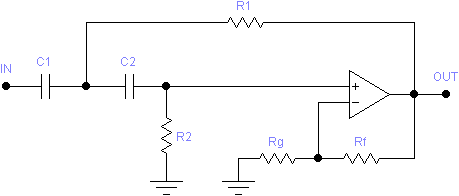
Subscribe Recommend		Low-Sensitivity Sallen-Key Filter Design with the HP-67 Programmable Calculator This program, a part of my series of analog electronic design programs for the HP-67 programmable calculator, addresses the problem of designing second order single op-amp low- and high-pass filters using the Sallen-Key topology. The Sallen-Key filter topology has the advantage of using a minimum of components. The simplest Sallen-Key filters use only two resistors and two capacitors. Additional resistors may be added for input attenuation (low-pass only) and gain adjustment. The following schematics illustrate these generalized Sallen-Key circuits: Generalized Sallen-Key low-pass filter Generalized Sallen-Key high-pass filter The equations governing the low-pass filter are as follows, where f is the filter's cut-off frequency, Q is its "quality", and H is its gain at the cut-off frequency. The corresponding equations for the high-pass filter are: The mathematically inclined will notice that in each case, there are three equations in either nine or ten variables. Thus there is no single "right" solution. At least six or seven of the variables have to be decided arbitrarily (f, Q, H, and three or four component values), at which point the remaining variables (component values) can be solved for. An article by Texas Instruments suggests a number of simplifications to help one choose component values, but this just adds the complication of which simplification to choose. I recently came across a pair of application notes by National Semiconductor which gives a procedure for designing Sallen-Key filters to minimize the effect of component value tolerances on the performance of the filter. A side-effect of this procedure is to reduce the number of inputs to five: f, Q, H, RF, and R, where the latter is simply an indication of the magnitude of resistor values desired for R1, R2, and R3. The procedure then dictates how all the other values are chosen, even adjusting for available "real-world" values part way through the solution. The program presented here implements this procedure, with some minor changes: Instead of asking for a desired resistor magnitude, R, the program asks for a capacitor magnitude, C, since in my experience, the capacitors drive the design. 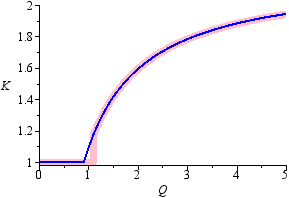The formula given for internal gain variable K in the procedure (please refer to the application note) seems to have been derived empirically, and has a jump at Q = 1.1. To make the formula simpler to implement, I modified it slightly to: The graphs of the original (pink) and revised (blue) formulae show the difference. Testing has shown that the resulting solution is generally at most one real-world capacitor value increment different (with corresponding changes in resistor values of course). Also, if H > K, then K is set equal to H, since otherwise it will not be possible to achieve the desired gain. For the low-pass circuit, the desired gain, H, is achieved by a combination of input attenuation, α (controlled by R1 and R3), and the internal gain, K, of the filter (controlled by RF and RG). The division of this gain between the two stages depends on H and Q and is chosen to minimize the sensitivity of the circuit to component tolerances. For example, for H = 1 and Q = 2, the attenuator gain is α = 0.629 and the internal gain is K = 1.59, for a net gain of H = αK = 1. The high-pass circuit has no attentuation stage, so H must be at least 1, and higher for Q > 0.917. If too low a value is entered for H, it is increased as necessary to make the circuit solvable. For either circuit, to achieve a result with minimum component sensitivity without regard to gain, set H = 0. The program will automatically choose the optimal value for K (and thus H). The resulting gain will be output when determining the performance. Using the Program First type in the program and save it, or read it from a previously recorded magnetic card. The card should be labelled as follows: LOW-SENSITIVITY SALLEN-KEY FILTER DESIGN f Q H C RF LP→RGC1C2R1R2R3   HP→RGC1C2R1R2   →f,Q,H Filter Design from Specifications Example: Design a 500Hz low-pass unity-gain filter with a Q of 2, using capacitors in the 10nF range, and a 47kΩ resistor for RF: Description Keystrokes Display Use engineering notation   h  ENG   DSP 2   0.00  00  Enter f  500    f  a   500.  00  Enter Q  2    f  b   2.00  00  Enter H  1    f  c   1.00  00  Enter C  10 EEx CHS 9    f  d   10.0 -09  Enter RF  47 EEx 3    f  e   47.0  03  Compute RG  A   79.5  03  Enter real-world RG and compute C1  82 EEx 3   R/S   31.6 -09  Enter real-world C1 and compute C2  33 EEx CHS 9   R/S   3.16 -09  Enter real-world C2 and compute R1  3.3 EEx CHS 9   R/S   15.4  03  Enter real-world R1 and compute R2  15 EEx 3   R/S   95.9  03  Enter real-world R2 and compute R3  100 EEx 3   R/S   26.1  03  Enter real-world R3  27 EEx 3   R/S   27.0  03  Notes If a resistor is to be omitted (open circuit), this program displays a value of zero for the resistance. This is different than some of my other programs, which display a "large" value representing infinity. When the value for RG is displayed as zero, meaning it can be omitted, the value of RF will not matter any more, and RF can be replaced by a direct connection. Filter Performance from Chosen Components During the calculation of the solution above, we've entered real-world values in response to each computed value. The real-world values of C1 and C2 are used when computing the values of R1, R2, and R3. However, the real-world values of each of those resistors does not affect the computed value of the remaining ones. Thus, the final filter may not perform exactly as specified. To find out how it does perform, follow these steps: Description Keystrokes Display Compute resulting f  E   491.  00  Compute resulting Q  R/S   1.86  00  Compute resulting H  R/S   1.01  00  A High-Pass Example Using the parameters already entered for the low-pass filter above, determine the components for a high-pass filter: Description Keystrokes Display Compute RG for high-pass filter  C   79.5  03  Enter real-world RG and compute C1  82 EEx 3   R/S   31.4 -09  Enter real-world C1 and compute C2  33 EEx CHS 9   R/S   3.18 -09  Enter real-world C2 and compute R1  3.3 EEx CHS 9   R/S   9.59  03  Enter real-world R1 and compute R2  10 EEx 3   R/S   97.0  03  Enter real-world R2  100 EEx 3   R/S   0.00  00  Now determine the predicted actual performance: Description Keystrokes Display Compute resulting f  E   482.  00  Compute resulting Q  R/S   1.96  00  Compute resulting H  R/S   1.57  00  Notice that H is higher than the specified unity gain. This is because the filter is not possible to construct with unity gain when Q = 2. The smallest possible gain is H = 1.59 (which due to real-world components, has become Q = 1.89 and H = 1.57). To achieve H = 1, you will need either a pre-attenuator with low output impedance, or a post-attenuator with high input impedance. Program Listing Line Instruction Comments 001♦   LBL a  Enter and store f 002  STO A    003  RTN    004♦   LBL b  Enter and store Q 005  STO B    006  RTN    007♦   LBL c  Enter and store H (gain) 008  STO C    009  RTN    010♦   LBL d  Enter and store C (capacitor scale) 011  STO 0    012  RTN    013♦   LBL e  Enter and store RF 014  STO 4    015  RTN    016♦   LBL A  Low-pass filter: RG,C1,C2,R1,R2,R3 017  CF 0    018  GTO 0    019♦   LBL C  High-pass filter: RG,C1,C2,R1,R2 020  SF 0    021♦   LBL 0  Forward solution 022  RCL B    023  2    024  .    025  2    026  ×    027  .    028  9    029  −    030  RCL B    031  .    032  2    033  +    034  ÷  (2.2Q-0.9)/(Q+0.2) 035  1    036  x≤y?    037  x↔y    038  STO E  K = max(1,(2.2Q-0.9)/(Q+0.2)) 039  RCL C    040  x>y?    041  STO E  K = max(H,1,(2.2Q-0.9)/(Q+0.2)) 042  RCL E    043  ÷  H/K 044  x=0?    045  1  Use α = 1 if H/K = 0 (because H was 0) 046  F? 0    047  1  Always use α = 1 for a high-pass filter 048  STO D  α = H/K (always 1 for a high-pass filter or H = 0) 049  RCL 4    050  RCL E    051  1    052  −    053  x≠0?    054  ÷  RG = RF/(K-1) if K ≠ 1, or zero if K = 1 055  R/S  Display RG and let user change it 056  STO 5    057  .  Initialize n to √0.1 058  1    059  √x    060  GSB 7  n(1+√(1+4Q2(1+n2)(K-1)))/(2Q(1+n2)) 061  RCL 8  √0.1 was stored here by subroutine 7 062  x≤y?    063  x↔y  max(n, n(1+√(1+4Q2(1+n2)(K-1)))/(2Q(1+n2))) 064  F? 0  High-pass filter? 065  GSB 6  2nQ/(1+√(1+4Q2(K-1-n2))) 066  STO 8    067  RCL 0    068  RCL 8    069  ÷  C1 = C/n 070  R/S  Display C1 and let user change it 071  STO 6    072  RCL 8    073  RCL 0    074  ×  C2 = nC 075  R/S  Display C2 and let user change it 076  STO 7    077  RCL 6    078  ×    079  √x  √(C1C2) 080  GSB 4  Multiply by 2πf and take reciprocal 081  STO 9  N = 1/(2πf√(C1C2)) 082  RCL 7    083  RCL 6    084  ÷    085  √x  n = √(C2/C1) 086  GSB 3  2nQ/(1+√(1+4Q2(K-1-n2))) or n(1+√(1+4Q2(1+n2)(K-1)))/(2Q(1+n2)) 087  STO 8    088  RCL 9    089  ×    090  STO 3  (R1||R3) = nN 091  RCL D    092  ÷  R1 = (R1||R3)/α 093  R/S  Display R1 and let user change it 094  STO 1    095  RCL 9    096  RCL 8    097  ÷  R2 = N/n 098  R/S  Display R2 and let user change it 099  STO 2    100  RCL 3    101  1    102  RCL D    103  −  ( 1-α (R1||R3) ) 104  x≠0?    105  ÷  R3 = (R1||R3)/(1-α) if α ≠ 1, or zero otherwise 106  R/S  Display R3 and let user change it 107  STO 3    108  RTN    109♦   LBL 4  Multiply by 2πf and take reciprocal 110  RCL A  f 111  ×    112♦   LBL 1  Multiply by 2π and take reciprocal 113  2    114  ×    115  π    116  ×    117  1/x    118  RTN    119♦   LBL 3  Compute either 2xQ/(1+√(1+4Q2(K-1-x2))) or x(1+√(1+4Q2(1+x2)(K-1)))/(2Q(1+x2)) 120  F? 0  High-pass filter? 121  GTO 7    122♦   LBL 6  Subroutine to compute 2xQ/(1+√(1+4Q2(K-1-x2))) 123  STO 8  Save x for later use 124  RCL B    125  2    126  ×  ( 2Q x ) 127  ×  ( 2xQ ) 128  LSTx  ( 2Q 2xQ ) 129  x2  ( 4Q2 2xQ ) 130  RCL E    131  1    132  −    133  RCL 8    134  x2    135  −  ( K-1-x2 4Q2 2xQ ) 136  ×  ( 4Q2(K-1-x2) 2xQ ) 137  GSB 9  ( 1+√(1+4Q2(K-1-x2)) 2xQ ) 138  ÷    139  RTN    140♦   LBL 7  Subroutine to compute x(1+√(1+4Q2(1+x2)(K-1)))/(2Q(1+x2)) 141  STO 8  Save x in register 8 for later use both by this subroutine and the caller 142  GSB 8  ( 2Q 1+x2 ) 143  x2    144  ×  ( 4Q2(1+x2) ) 145  RCL E    146  1    147  −  ( K-1 4Q2(1+x2) ) 148  ×  ( 4Q2(1+x2)(K-1) ) 149  GSB 9  ( 1+√(1+4Q2(1+x2)(K-1)) ) 150  RCL 8    151  ×  ( x(1+√(1+4Q2(1+x2)(K-1))) ) 152  RCL 8    153  GSB 8  ( 2Q 1+x2 x(1+√(1+4Q2(1+x2)(K-1))) ) 154  ×  ( 2Q(1+x2) x(1+√(1+4Q2(1+x2)(K-1))) ) 155  ÷    156  RTN    157♦   LBL 8  Subroutine to populate stack with 2Q 1+x2 158  x2    159  1    160  +    161  RCL B    162  2    163  ×    164  RTN    165♦   LBL 9  Subroutine to compute 1+√(1+x) 166  1    167  +    168  √x    169  1    170  +    171  RTN    172♦   LBL E  Compute actual f, Q, and Gain 173  GSB 2  R1 or (R1||R3) 174  RCL 6    175  ×    176  STO 8  Save R1C1 for use in calculating Q 177  RCL 2    178  RCL 7    179  ×    180  STO 9  Save R2C2 for use in calculating Q 181  ×    182  √x    183  GSB 1  Multiply by 2π and take reciprocal 184  ST I  Save actual f for use in calculating Q 185  R/S  Display actual f 186  RCL 9  ( R2C2 ) 187  RCL 8  ( R1C1 R2C2 ) 188  F? 0  High-pass filter? 189  x↔y  ( R2C2 R1C1 ) 190  1    191  RCL E    192  −    193  ×    194  +    195  GSB 2  R1 or (R1||R3) 196  RCL 7    197  ×    198  +    199  RC I  Recall actual frequency 200  ×    201  GSB 1  Multiply by 2π and take reciprocal 202  R/S  Display actual Q 203  RCL 4    204  RCL 5    205  x≠0?    206  ÷    207  1    208  +    209  GSB 2  R1 or (R1||R3) 210  ×    211  RCL 1    212  ÷    213  RTN  Return actual Gain 214♦   LBL 2  Return either R1 or (R1||R3) 215  RCL 1    216  F? 0  High-pass filter? 217  RTN  Return just R1 218  1/x    219  RCL 3    220  x≠0?  R3 exists? (0 means not) 221  1/x    222  +    223  1/x    224  RTN    Registers and Flags Register Use  0  C - capacitor scale  1,2,3  R1, R2, R3 - filter resistors  4,5  RF, RG - feedback resistors  6,7  C1, C2 - capacitors  8  n - variable used during computation  9  N - variable used during computation  A  f - cutoff frequency  B  Q - filter quality  C  H - overall gain  D  α - input attenuator gain  E  K - internal gain  I  Temporary register Flag Meaning  0  High-pass filter Revision History 2008-Dec-12 — Initial release. References 1. Analysis of the Sallen-Key Architecture (Rev.B), Texas Instruments Application Report SLOA024B, James Karki, 2002 2. Low-Sensitivity, Lowpass Filter Design, National Semiconductor Application Note OA-27, Kumen Blake, 1996 3. Low-Sensitivity, Highpass Filter Design, National Semiconductor Application Note OA-29, Kumen Blake, 1996 Other HP Calculator Programs I've written programs for many of the HP calculators calculators in my collection. You may be interested in some of these: HP 35s Curve Fitting Matrix Multi-Tool HP-41C/CV/CX Low-Sensitivity Sallen-Key Filter Design Op-Amp Gain and Offset Stage Design Op-Amp Oscillator Design HP-67 Op-Amp Gain and Offset Stage Design Op-Amp Oscillator Design Resistor Networks of 1 or 2 Nodes     Buy Stefan a coffee! If you've found this article useful, consider leaving a donation to help support stefanv.com   Last updated Monday May 25, 2009. E-mail Stefan   Disclaimer: Although every effort has been made to ensure accuracy and reliability, the information on this web page is presented without warranty of any kind, and Stefan Vorkoetter assumes no liability for direct or consequential damages caused by its use. It is up to you, the reader, to determine the suitability of, and assume responsibility for, the use of this information. Copyright: All materials on this web site, including the text, images, and HTML mark-up, are Copyright © 2009 by Stefan Vorkoetter unless otherwise noted. All rights reserved. Unauthorized duplication prohibited. You may link to this site or pages within it, but you may not link directly to images on this site, and you may not copy any material from this site to another web site or other publication without express written permission. You may make copies for your own personal use.