Op-Amp Gain and Offset Design with the HP-67 Programmable Calculator
December 4, 2008
This is the third in an ongoing series of electronic design programs that I’m writing for the HP-67. This program is for designing offset-and-gain stages using a single operational amplifier. Such stages are often necessary to convert an input signal covering one range of voltages (e.g., 0.1V to 0.2V from a sensor) to an output signal covering a different range (e.g., 1.0 to 4.0V into an A/D converter).
Mathematically, such a stage performs a linear transformation on the input voltage,
VOUT = m VIN + b
where m is the slope and b is the intercept or offset.
Given an input voltage range, VIL to VIH, and an output voltage range, VOL to VOH, the slope and offset are given by:
There are four main cases to consider, with different circuits for each, that are addressed by this program:
- Positive slope and offset (m > 0 and b > 0)
- Positive slope and negative offset (m > 0 and b < 0)
- Negative slope and positive offset (m < 0 and b > 0)
- Negative slope and offset (m < 0 and b < 0)
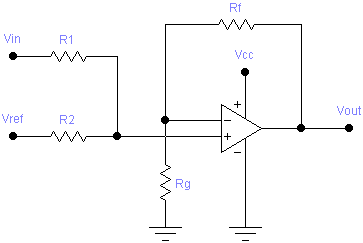
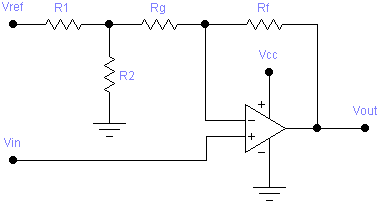
Positive Slope and Offset
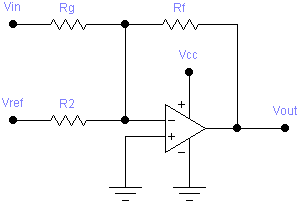
A positive slope and offset stage is implemented by the following circuit:
The designer must select values for R1 and RF, and then appropriate values for R2 and RG can be calculated using the following formulae:
After determining theoretically ideal values for R2 and RG, real-world values can be chosen and the following formula applied to VIL and VIH to see the resulting values of VOL and VOH respectively:
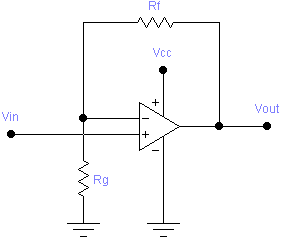
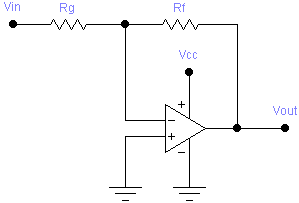
This case is also used to handle the special case where b = 0 (postive gain with no offset). In such a case, the formula for R2 would result in dividing by zero, which means R2 is infinite. In other words, R2 and VREF are not needed. The value of R1 won’t matter then either, and can be replaced by a direct connection. The circuit reduces to:
Positive Slope and Negative Offset
The following circuit implements a positive slope and negative offset stage:
After choosing values for R1 and RF, values for R2 and RG can be be calculated using these formulae:
The following formula can then be used to determine the effect of real-world values of R2 and RG on the transformation:
Negative Slope and Positive Offset
A negative slope and postive offset stage is implemented by the following circuit:
Given values for R1 and RF, values for R2 and RG can be be calculated as follows:
The following formula can then be used to determine the effect of substituting real-world values of R2 and RG:
This case is also used to handle the special case where b = 0 (negative gain with no offset). As in case 1, the formula for R2 would involve division by zero, so R2 and VREF are not needed. The non-inverting input of the op-amp can be connected directly to ground, giving the following circuit:
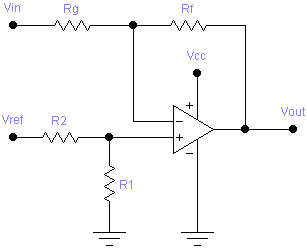
Negative Slope and Offset
The following circuit implements a negative slope and offset stage:
This circuit has no R1, so it is only necessary to choose a value for RF, after which R2 and RG are given by:
The effect of using real-world values of R2 and RG can then be tested using this formula:
Limitations
Theoretically, the formulae presented here work perfectly well for gains between -1 and 1 (i.e. |m| < 1). However, many real-world op-amps are unstable in such cases. Instead, it will usually be necessary to design for a higher gain (|m| ≥ 1), with an attenuator on the input side. The design procedures for this are described on Texas Instruments’ Op Amp Gain and Offset Page.
Using the Program
First type in the program and save it, or read it from a previously recorded magnetic card. The card should be labelled as follows:
| OP-AMP GAIN AND OFFSET STAGE DESIGN | ||||
|---|---|---|---|---|
| VREF | VIL,VIH | VOL,VOH | ||
| →m,b | →CASE | R1,RF→R2,RG | R2,RG→VOL,VOH | |
Forward Solution: Finding R2 and RG
Consider the following example. A sensor has an output ranging from 0.5V to 0.7V, and we want to interface it to an A/D converter that is expecting an input between 1V and 4V. There is no reference voltage available other than the well regulated 5V supply voltage of the circuit. Use a 10kΩ resistor for R1, and 100kΩ for RF.
Follow these steps to solve the problem:
| Description | Keystrokes | Display |
|---|---|---|
| Use engineering notation | h ENG DSP 2 |
0.00 00 |
| Enter VREF | 5 f a |
5.00 00 |
| Enter VIL and VIH | 0.5 ENTER 0.7 f b |
500. -03 |
| Enter VOL and VOH | 1 ENTER 4 f c |
1.00 00 |
| Compute slope m | A | 15.0 00 |
| Compute offset b | R/S | -6.50 00 |
| Determine case number | B | 2.00 00 |
| Enter R1 and RF, compute R2 | 10 EEx 3 ENTER 100 EEx 3 C |
1.02 03 |
| Compute RG | R/S | 6.21 03 |
Notes
It is not necessary to compute the slope and offset (by pressing A) before determining the case number. Likewise, it isn’t necessary to determine the case number (by pressing B) before computing resistor values (although you’ll want to know the case number in order to know which circuit to build). The program keeps track of which information is up to date, and will (re)compute anything that it needs that hasn’t already been computed.
Reverse Solution: Finding the Effect of R2 and RG on VOL and VOH
The closest available 5% resistor values for R2 and RG are 1kΩ and 6.2kΩ respectively. What effect does using these have on the solution? Follow these steps to find out:
| Description | Keystrokes | Display |
|---|---|---|
| Enter R2 and RG, compute VOL | 1 EEx 3 ENTER 6.2 EEx 3 D |
1.13 00 |
| Compute VOH | R/S | 4.15 00 |
This is within the A/D’s input range at the lower bound, but outside the range at the upper bound. What happens if we use the next available value for RG, 6.8kΩ, instead?
| Description | Keystrokes | Display |
|---|---|---|
| Enter R2 and RG, compute VOL | 1 EEx 3 ENTER 6.8 EEx 3 D |
1.09 00 |
| Compute VOH | R/S | 3.88 00 |
This is almost centered within the desired output range, and covers 93% of it.
The only remaining concern is how component tolerances might affect the solution. This can be analyzed by trying different combinations of R1, R2, RF, and RG representing resistors that are maximally out of tolerance (±5%) in each direction.
For example, to test the case where R1 and RF are 5% low and R2 and RG are 5% high, follow these steps:
| Description | Keystrokes | Display |
|---|---|---|
| Enter low R1 and RF, ignore computed R2 | 0.95 EEx 3 ENTER 95 EEx 3 C |
920. 00 |
| Enter high R2 and RG, compute VOL | 1.05 EEx 3 ENTER 7.14 EEx 3 D |
808. -03 |
| Compute VOH | R/S | 3.48 00 |
The results show that in this case, the lower limit of the output is out of range, meaning either a redesign is necessary, or tighter tolerance components are needed.
Cases where b = 0
In cases where the offset, b, is zero, the program will instead use b = 10-9 as the offset. This will avoid any division-by-zero errors. The program will then use case 1 (if m > 0) or case 3 (if m < 0) to compute the solution. In both cases, the computed value for R2 will be very large, typically around 109 times the value specified for R1. This indicates that R2 and VREF can be omitted, and that R1 can be replaced by a direct connection.
Program Listing
| Line | Instruction | Comments |
|---|---|---|
| 001♦ | LBL a | Enter available reference voltage |
| 002 | STO 9 | |
| 003 | RTN | |
| 004♦ | LBL b | Enter VIL and VIH |
| 005 | STO 6 | Store VIH |
| 006 | x↔y | |
| 007 | STO 5 | Store VIL |
| 008 | CF 0 | Must recompute m and b |
| 009 | RTN | |
| 010♦ | LBL c | Enter VOL and VOH |
| 011 | STO 8 | Store VOH |
| 012 | x↔y | |
| 013 | STO 7 | Store VOL |
| 014 | CF 0 | Must recompute m and b |
| 015 | RTN | |
| 016♦ | LBL A | Compute transfer function slope (m) and intercept (b) |
| 017 | F? 0 | Are m and b already up to date? |
| 018 | GTO 5 | |
| 019 | RCL 8 | Compute and store m = (VOH – VOL) ÷ (VIH – VIL) |
| 020 | RCL 7 | |
| 021 | − | |
| 022 | RCL 6 | |
| 023 | RCL 5 | |
| 024 | − | |
| 025 | ÷ | |
| 026 | STO A | |
| 027 | RCL 5 | Compute and store b = VOH – m VIL |
| 028 | × | |
| 029 | RCL 7 | |
| 030 | − | |
| 031 | CHS | |
| 032 | x≠0? | |
| 033 | GTO 7 | |
| 034 | EEx | Make sure b is never exactly 0 |
| 035 | CHS | |
| 036 | 9 | |
| 037♦ | LBL 7 | |
| 038 | STO B | |
| 039 | SF 0 | Stored m and b are now up to date |
| 040 | CF 1 | Must recompute case number now |
| 041♦ | LBL 5 | Display computed or already up-to-date m and b |
| 042 | RCL A | |
| 043 | RTN | Return, leaving m on stack |
| 044 | RCL B | Display b if user pressed R/S after return |
| 045 | RTN | |
| 046♦ | LBL B | Compute case number and store in I |
| 047 | GSB A | Make sure m and b are up to date |
| 048 | F? 1 | Is case number already up to date |
| 049 | GTO 8 | |
| 050 | x<0? | |
| 051 | GTO 6 | Handle cases where m < 0 |
| 052 | 1 | |
| 053 | ST I | |
| 054 | RCL B | |
| 055 | x<0? | |
| 056 | ISZ I | Case 2: m positive and b negative |
| 057 | GTO 8 | Case 1: m positive and b positive |
| 058♦ | LBL 6 | Cases where m is negative |
| 059 | 3 | |
| 060 | ST I | |
| 061 | RCL B | |
| 062 | x<0? | |
| 063 | ISZ I | Case 4: m negative and b negative |
| 064♦ | LBL 8 | Case 3: m negative and b positive |
| 065 | SF 1 | Case number is now up to date (or was already up to date) |
| 066 | RC I | Display case number and return |
| 067 | RTN | |
| 068♦ | LBL C | Compute solution using appropriate case |
| 069 | STO 3 | Store RF |
| 070 | x↔y | |
| 071 | STO 1 | Store R1 |
| 072 | GSB B | Get case number |
| 073 | GTO (i) | Branch to appropriate case |
| 074♦ | LBL 1 | Positive m and positive b |
| 075 | RCL 1 | Compute and store R2 = VREF R1 m ÷ b |
| 076 | RCL 9 | |
| 077 | × | |
| 078 | RCL A | |
| 079 | × | |
| 080 | RCL B | |
| 081 | ÷ | |
| 082 | STO 2 | |
| 083 | R/S | Display R2; 9.99e99 means “open circuit” |
| 084 | RCL 9 | Compute and store RG = VREF RF ÷ (VREF (m – 1) + b) |
| 085 | RCL 3 | |
| 086 | × | |
| 087 | GSB 9 | Compute VREF (m – 1) + b |
| 088 | GTO 5 | Divide, store RG, and return, leaving RG on stack |
| 089♦ | LBL 2 | Positive m and negative b |
| 090 | RCL 1 | Compute and store R2 = –R1 b ÷ (VREF (m – 1) + b) |
| 091 | RCL B | |
| 092 | CHS | |
| 093 | × | |
| 094 | GSB 9 | Compute VREF (m – 1) + b, leaving VREF (m – 1) in register 0 |
| 095 | ÷ | |
| 096 | STO 2 | |
| 097 | R/S | Display R2 |
| 098 | RCL 1 | Compute and store RG = (R1 b + VREF RF) ÷ (VREF (m – 1)) |
| 099 | RCL B | |
| 100 | × | |
| 101 | RCL 9 | |
| 102 | RCL 3 | |
| 103 | × | |
| 104 | + | |
| 105 | RCL 0 | Subroutine 9 left VREF (m – 1) in register 0 for us |
| 106 | GTO 5 | Divide, store RG, and return, leaving RG on stack |
| 107♦ | LBL 3 | Negative m and positive b |
| 108 | RCL 1 | Compute and store R2 = R1 (VREF (m – 1) + b) ÷ –b |
| 109 | GSB 9 | Compute VREF (m – 1) + b |
| 110 | × | |
| 111 | RCL B | |
| 112 | CHS | |
| 113 | ÷ | |
| 114 | STO 2 | |
| 115 | R/S | Display R2 |
| 116 | RCL 3 | Compute and store RG = –RF ÷ m |
| 117 | CHS | |
| 118 | RCL A | |
| 119 | GTO 5 | Divide, store RG, and return, leaving RG on stack |
| 120♦ | LBL 4 | Negative m and negative b |
| 121 | RCL 9 | Compute and store R2 = VREF RF ÷ –b |
| 122 | RCL 3 | |
| 123 | × | |
| 124 | RCL B | |
| 125 | CHS | |
| 126 | ÷ | |
| 127 | STO 2 | |
| 128 | R/S | Display R2 |
| 129 | RCL 3 | Compute and store RG = RF ÷ m |
| 130 | RCL A | |
| 131 | CHS | |
| 132♦ | LBL 5 | Common code to compute y ÷ x and store in RG |
| 133 | ÷ | |
| 134 | STO 4 | |
| 135 | RTN | Return, leaving RG on stack |
| 136♦ | LBL 9 | Compute VREF (m – 1) + b, leaving VREF (m – 1) in register 0 |
| 137 | RCL A | |
| 138 | 1 | |
| 139 | − | |
| 140 | RCL 9 | |
| 141 | × | |
| 142 | STO 0 | Save VREF (m – 1) in register 0 for later |
| 143 | RCL B | |
| 144 | + | |
| 145 | RTN | |
| 146♦ | LBL D | Compute VOL,VOH using supplied R2,RG |
| 147 | STO 4 | Store RG |
| 148 | x↔y | |
| 149 | STO 2 | Store R2 |
| 150 | GSB B | Get case number |
| 151 | RCL 5 | |
| 152 | GSB (i) | Compute VOL from VIL |
| 153 | R/S | Display computed VOL |
| 154 | RCL 6 | |
| 155 | GTO (i) | Compute VOH from VIH |
| 156♦ | LBL 1 | Compute VOUT for positive m and positive b |
| 157 | RCL 2 | |
| 158 | × | |
| 159♦ | LBL 0 | Entry point to compute (x + VREF R1) (1 + RF ÷ RG) ÷ (R1 + R2) |
| 160 | RCL 9 | |
| 161 | RCL 1 | |
| 162 | × | |
| 163 | + | |
| 164 | RCL 3 | |
| 165 | RCL 4 | |
| 166 | ÷ | |
| 167 | 1 | |
| 168 | + | |
| 169 | × | |
| 170 | RCL 1 | |
| 171 | RCL 2 | |
| 172 | + | |
| 173 | ÷ | |
| 174 | RTN | |
| 175♦ | LBL 2 | Compute VOUT for positive m and negative b |
| 176 | RCL 1 | |
| 177 | 1/x | |
| 178 | RCL 2 | |
| 179 | 1/x | |
| 180 | + | |
| 181 | 1/x | |
| 182 | RCL 4 | |
| 183 | + | |
| 184 | STO 0 | Store RG + R1 R2 ÷ (R1 + R2) for later |
| 185 | RCL 3 | |
| 186 | + | |
| 187 | × | |
| 188 | RCL 0 | |
| 189 | ÷ | |
| 190 | RCL 9 | |
| 191 | RCL 2 | |
| 192 | × | |
| 193 | RCL 3 | |
| 194 | × | |
| 195 | RCL 1 | |
| 196 | RCL 2 | |
| 197 | + | |
| 198 | RCL 0 | |
| 199 | × | |
| 200 | ÷ | |
| 201 | − | |
| 202 | RTN | |
| 203♦ | LBL 3 | Compute VOUT for negative m and positive b |
| 204 | 0 | |
| 205 | GSB 0 | Compute (VREF R1) (1 + RF ÷ RG) ÷ (R1 + R2) |
| 206 | GTO 9 | Subtract VIN RF ÷ RG |
| 207♦ | LBL 4 | Compute VOUT for negative m and negative b |
| 208 | RCL 9 | |
| 209 | RCL 3 | |
| 210 | × | |
| 211 | RCL 2 | |
| 212 | ÷ | |
| 213 | CHS | |
| 214♦ | LBL 9 | Entry point to compute x – y RF ÷ RG |
| 215 | x↔y | |
| 216 | RCL 3 | |
| 217 | × | |
| 218 | RCL 4 | |
| 219 | ÷ | |
| 220 | − | |
| 221 | RTN |
Two interesting aspects of this program are its use of indirect addressing for branching to the forward and reverse solution subroutines for each of the four cases, and its use of repeated labels.
The forward solution for each of the four slope/offset cases is implemented by a sequence of instructions starting with the label corresponding to the case number (1 to 4). When the user presses C, the case number is computed if necessary, and a GTO (i) instruction then branches to the appropriate case.
Similarly, the reverse solution for each case is also labeled according to the case number. When the user presses D, VIL is recalled to the stack, after which a GSB (i) instruction causes VOL to be calculated. Then VIH is recalled, and GTO (i) is used to calculate VOH and then return.
So, there are two each of LBL 1 through LBL 4. This works because the HP-67 (and other vintage HP calculators) search forwards from the current step for the matching label. Thus the GTO (i) in step 73 will branch to the appropriate forward solution, and the GSB (i) in step 152 and GTO (i) in step 155 will branch to the appropriate reverse solution.
This program also makes use of many small subroutines to compute sub-expressions common to multiple solutions. Since there were not enough labels for all the subroutines needed, the same labels were used more than once. Had this not been done, the same sequence of steps would have been repeated several times, and the program would not have fit into the calculator’s 224 step memory.
Registers and Flags
| Register | Use |
|---|---|
| 0 | Temporary register |
| 1 | R1 (Ohms) |
| 2 | R2 (Ohms) |
| 3 | RF (Ohms) |
| 4 | RG (Ohms) |
| 5,6 | VIL and VIH, input voltage range |
| 7,8 | VOL and VOH, output voltage range |
| 9 | VREF |
| A | m, slope of transfer function |
| B | b, intercept of transfer function |
| I | Case number (1,2,3,4) |
| Flag | Meaning |
|---|---|
| 0 | m and b are up to date |
| 1 | Case number is up to date |
Revision History
2008-Dec-04 — Initial release.
Related Articles
If you've found this article useful, you may also be interested in:
- Op-Amp Gain and Offset Design with the HP-41C Programmable Calculator
- Op-Amp Oscillator Design with the HP-41C Programmable Calculator
- Low-Sensitivity Sallen-Key Filter Design with the HP-41C Programmable Calculator
- Low-Sensitivity Sallen-Key Filter Design with the HP-67 Programmable Calculator
- Op-Amp Oscillator Design with the HP-67 Programmable Calculator
- Resistor Network Solver for the HP-67 Programmable Calculator
- A Matrix Multi-Tool for the HP 35s Programmable Calculator
- Curve Fitting for the HP 35s Programmable Calculator

If you've found this article useful, consider leaving a donation in Stefan's memory to help support stefanv.com
Disclaimer: Although every effort has been made to ensure accuracy and reliability, the information on this web page is presented without warranty of any kind, and Stefan Vorkoetter assumes no liability for direct or consequential damages caused by its use. It is up to you, the reader, to determine the suitability of, and assume responsibility for, the use of this information. Links to Amazon.com merchandise are provided in association with Amazon.com. Links to eBay searches are provided in association with the eBay partner network.
Copyright: All materials on this web site, including the text, images, and mark-up, are Copyright © 2025 by Stefan Vorkoetter unless otherwise noted. All rights reserved. Unauthorized duplication prohibited. You may link to this site or pages within it, but you may not link directly to images on this site, and you may not copy any material from this site to another web site or other publication without express written permission. You may make copies for your own personal use.
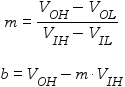
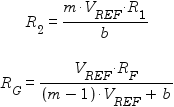

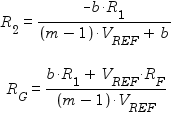
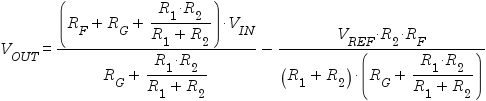
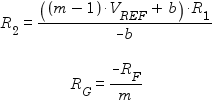
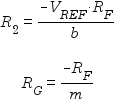
Saim Sharik
November 25, 2010
opamp
Willy Kunz
May 15, 2013
I entered the program into my iPad HP-67 emulator (“RPN-67 Pro”) and got a few differing results. Specifically, in section “Reverse Solution: Finding the Effect of R2 and RG on VOL and VOH” the first result was 1.14 instead of 1.13. More seriously, the last three results were totally off the mark:
97.2 instead of 920, -25.9 instead of 808, and -23.2 instead of 3.48. After checking the listing several times, I entered the program into a physical HP-67. It returned results in exact agreement with the emulator. I suspect there’s a typo in the listing, but I haven’t figured it out yet.
Stefan Vorkoetter
May 15, 2013
I’ll have to double check the listing against the actual program. Thing is, I develop HP programs using a text editor, and then enter the program and generate the listings for my articles from the same original source, so I’m not sure how an error could have crept in. But anything’s possible.
Willy Kunz
May 16, 2013
It seems the listing is okay. What’s wrong is the value entered for low R1 in the example. Instead of 0.95 EEx 3 it should be 9.5 EEx 3. The resulting display then is 972. 00 (not 920. 00). VOL will be 512.-03 (not 808.-03) and VOH will be 3.08 00 (not 3.48 00).
(Stefan, please contact me by e-mail.)
gabdsung
January 11, 2024
m is positive always.