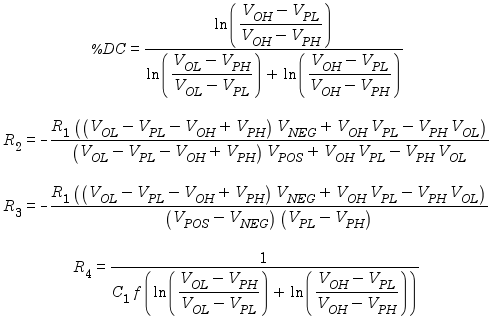Op-Amp Oscillator Design with the HP-41C Programmable Calculator

May 25, 2009

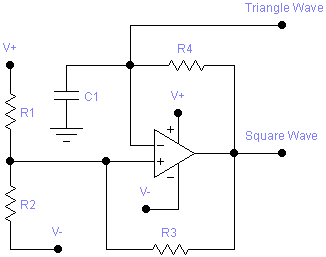
I originally wrote this program for the HP-67 calculator, and then ported it to the HP-41C series. This program selects component values for an op-amp based relaxation oscillator, given the desired frequency and output wave form peak voltages. It can also solve the inverse problem, finding the frequency and voltages resulting from given component values. The following is the schematic for such an oscillator:

R₁ and R₂ form a voltage divider, with an additional input from the op-amp output through R₃. When the op-amp output is at a high-level, the voltage at the non-inverting input of the op-amp is higher than when the op-amp output is at a low level. When the output is high, capacitor C₁ also charges through R₄ until the voltage across it (which is applied to the op-amp’s inverting input) reaches the voltage at the non-inverting input. At that time, the op-amp output goes low, and the capacitor begins to discharge through R₄ until the voltage once again reaches the (now lower) voltage at the non-inverting input.

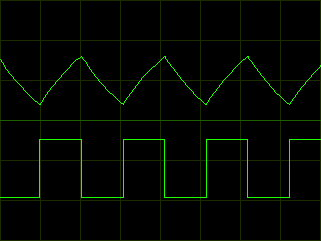
If one were to monitor the op-amp output, it would alternate between a high level (V_OH, generally close to positive supply voltage, V_POS) and a low level (V_OL, generally close to negative supply voltage, V_NEG). The duty cycle of this square wave depends on the relative time it takes to charge and discharge C₁ through R₄, which in turn depends on the low (V_PL) and high (V_PH) peak voltages that C₁ cycles between (which in turn depend on R₁, R₂, and R₃). Monitoring the voltage across C₁ shows a triangle wave.

With this program, you can select components for such an oscillator to achieve a desired frequency, and if it matters to your design, desired low and high triangle peaks (V_PL and V_PH). After the program computes the required component values, you can modify these values to match those actually available in the real world. The program will then compute what effect these changes have on the frequency and triangle peak voltages.

The following equations describe the operation of the oscillator:

You will first need to choose values for C₁ and R₁ arbitrarily, since for any desired frequency and given C₁ and R₁, it will be possible to find (possibly impractical) values for R₂, R₃, and R₄. A good choice for R₁ is generally somewhere around 10kΩ to 100kΩ. The choice of C₁ depends on the frequency, and a readily available value near (50/f) μF is usually suitable.

Using the Program

First type in the program and save it, or read it from a previously recorded magnetic card. The card should be labelled as follows:

OP-AMP OSCILLATOR DESIGN
VNEG,VPOS	VOL,VOH	C1	R1	VPL,VPH
f	→%DC	→R2→	→R3→	→R4→

Forward Solution: Finding R₂, R₃, and R₄

Consider the following example: It is desired to find values for R₂, R₃, and R₄ to produce an oscillator of about 2500Hz, with a triangle waveform that oscillates between 1.2V and 1.4V. The op-amp is to operate from a single 5V supply, and the op-amp’s output is capable of a low of 0.3V and a high of 5V. Use a 0.022μF capacitor for C₁, and a 22kΩ resistor for R₁.

Follow these steps to solve the problem:

Description	Keystrokes	Display
Select engineering notation	ENG 2	0.00  00
Enter power supply voltages	0 ENTER 5       a	0.00  00
Enter low and high level output voltages	0.3 ENTER 5       b	300. -03
Enter C1 (Farads)	0.022 EEx CHS 6       c	22.0 -09
Enter R1 (Ohms)	22 EEx 3       d	22.0  03
Enter desired triangle lower and upper voltage peaks	1.2 ENTER 1.4       e	1.20  00
Enter desired frequency (Hz)	2500   A	2.50  03
Compute square wave duty cycle	B	788. -03
Compute value of R2 (Ohms)	C	7.26  03
Compute value of R3 (Ohms)	D	123.  03
Compute value of R4 (Ohms)	E	71.4  03

Notes

Specifying V_OL and V_OH is optional. If this step is omitted, the program will assume the op-amp output can span the entire negative and positive supply voltage range.

If the triangle wave form peak voltages don’t matter to your design (because you’re only using the square wave output), you don’t need to specify them. The program will assume peak voltages ranging from V_OL+(V_OH–V_OL)/3 to V_OH-(V_OH–V_OL)/3, which is the middle third of the op-amp output voltage range. This also happens to result in a 50% duty cycle.

To achive a low duty cycle square wave, choose V_PL and V_PH close to the bottom of the op-amp output range (V_OL). Likewise for a high duty cycle, choose V_PL and V_PH close to the top of the range (V_OH).

For the most stable oscillation frequency, choose V_PL and V_PH far away from the op-amp output voltage limits, V_OL and V_OH (to keep the triangle edges steep), and far away from each other (to keep any variations a small percentage of the overall voltage swing). Since these two goals are at odds with one another, a good compromise is to select V_PL and V_PH to span the middle of the V_OL to V_OH range (which is the default if V_PL and V_PH aren’t specified).

Reverse Solution: Finding V_PL, V_PH, Frequency, and Duty Cycle

After finding the above ideal solution, we’ll want to use real-world component values to build the physical circuit. The closest E-24 resistor values to those computed are: R₂ = 7.5kΩ, R₃ = 120kΩ, and R₄ = 68kΩ. What effect will using these values have on the frequency, V_PL, and V_PH?

These are the steps to find out:

Description	Keystrokes	Display
Enter new value for R2	7.5 EEx 3   C	7.50 03
Enter new value for R3	120 EEx 3   D	120. 03
Enter new value for R4	68 EEx 3   E	68.0 03
Compute resulting value for VPL	e	1.23 00
Compute resulting value for VPH	R/S	1.44 00
Compute resulting frequency	A	2.57 03

Other Uses for this Program

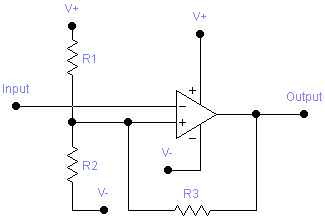
The oscillator design facilitated by this program consists of two parts, a comparator with hysteresis, and a capacitor being charged and discharged by the comparator output through a resistor. The equations describing the comparator aspect of the circuit are not affected by those describing the behaviour of the resistor-capacitor network, so the program can be used to design such comparators for other applications.

Here is a brief example of using this program to design a comparator: Assume we want to design a comparator operating from a +/-12V supply, whose output goes low when the voltage exceeds +2V, and goes high when the voltage subsequently drops below -3V. Assume the op amp used has an output that can swing to within 0.7V of the voltage limits. Use a 10kΩ resistor for R₁. Follow these steps to solve the problem:

Description	Keystrokes	Display
Enter power supply voltages	12 CHS ENTER 12       a	-12.0 00
Enter low and high level output voltages	11.3 CHS ENTER 11.3       b	-11.3 00
Enter R1	10 EEx 3       d	10.0 03
Enter desired lower and upper switching points	3 CHS ENTER 2       e	-3.00 00
Compute value of R2	C	8.98 03
Compute value of R3	D	16.7 03

Now select the closest real-world resistor values for R₂ and R₃ and determine how that affects the switching points:

Description	Keystrokes	Display
Enter new value for R2	9.1 EEx 3   C	9.10 03
Enter new value for R3	16 EEx 3   D	16.0 03
Compute resulting lower switching point	e	-3.03 00
Compute resulting upper switching point	R/S	2.16 00

Additional Real-World Considerations

The mathematical model used as the basis of this program assumes that V_OL and V_OH are constant, regardless of load. For sufficiently low current, this is close enough to true to be ignored. Thus it is important to use fairly high resistor values for R₃ and R₄ (10kΩ or bigger to be on the safe side). If the value of R₃ computed by the program is too low, start with a higher value for R₁. Similarly, if the value computed for R₄ is too low, use a lower value for C₁.

Some op-amps have an open-collector output. This means that when the output is low, it is pulled low through an output transistor, but when the output is high, it is simply floating. Thus, a pull-up resistor is needed to pull the output high. The chosen pull-up resistor must meet two requirements:

1. It must have a high-enough resistance that the output transistor can overcome the pull-up current when the output is low.

2. It must have a low-enough resistance that it is not so large a percentage of the resistance of R₃ or R₄ that it throws off the solution.

For the LM339 comparator that I often use in my designs, I’ve found that a 1kΩ resistor works well, together with R₃ and R₄ values about 100 times as much. As described above, use a higher value for R₁ to achieve a higher value for R₃, and use a lower value for C₁ to achieve a higher R₄.

Program Listing

Line	Instruction	Comments
01♦	LBL “OSC”
02♦	LBL a	Store VNEG and VPOS
03	STO 06	VPOS
04	x↔y
05	STO 05	VNEG
06	x↔y	Fall through and initialize VOL and VOH to VNEG and VPOS
07♦	LBL b	Store VOL and VOH
08	CF 22
09	STO 08	VOH
10	x↔y
11	STO 07	VOL
12	−	Initialize VPL and VPH
13	3
14	÷	(VOH–VOL)/3
15	RCL 07
16	x↔y
17	+
18	STO 11	Set VPL = VOL + (VOH–VOL)/3
19	RCL 08
20	LASTx
21	−
22	STO 12	Set VPH = VOH – (VOH–VOL)/3
23	CF 01
24	RCL 08	Leave VOL and VPH on stack as feedback to user
25	RCL 07
26	RTN
27♦	LBL c	Store C1
28	CF 22
29	STO 13
30	RTN
31♦	LBL d	Store R1
32	CF 22
33	STO 01
34	RTN
35♦	LBL e	Store or compute (if necessary) VPL and VPH
36	FS?C 22	If data entered, store new VPL and VPH
37	GTO 09
38♦	LBL 01	Otherwise, compute VPL and VPH if necessary
39	FS? 01	Need to compute VPL and VPH?
40	GTO 08
41	RCL 12	Recall already-up-to-date VPL and VPH
42	RCL 11
43	RTN
44	RCL 12	If user presses R/S after seeing VPL, display VPH
45	RTN
46♦	LBL 08	Recompute VPL and VPH
47	RCL 01
48	RCL 03
49	×
50	STO 14
51	RCL 02
52	RCL 03
53	×
54	STO 10
55	+
56	RCL 02
57	RCL 01
58	×
59	STO 09
60	+
61	1/x
62	STO 15
63	RCL 05
64	×
65	RCL 14
66	×
67	RCL 15
68	RCL 06
69	×
70	RCL 10
71	×
72	+
73	STO 14	Partial result common to VPL and VPH
74	RCL 15
75	RCL 09
76	×
77	STO 15	End of computation common to VPL and VPH
78	RCL 07	Compute VPL
79	×
80	+	End of computation of VPL
81	RCL 15	Compute VPH
82	RCL 08
83	×
84	RCL 14
85	+	End of computation of VPH; VPL is in Y-register
86♦	LBL 09	Store entered or computed VPH and VPL
87	STO 12	Store VPH
88	x↔y
89	STO 11	Store VPL
90	CF 01	VPL and VPH are now up to date
91	RTN
92	RCL 12	If user presses R/S after seeing VPL, display VPH
93	RTN
94♦	LBL B	Compute duty cycle
95	CF 22
96	XEQ 07	Get numerator and denominator (also used for computing R4 or f)
97	LASTx	Numerator
98	x↔y
99	÷
100	RTN
101♦	LBL 07	Compute denominator of duty cycle, leaving numerator in LSTx
102	XEQ 01	Recompute VPL and VPH if necessary; leaves VPH in X, VPL in Y
103	RCL 08	Compute first half of denominator
104	−
105	RCL 12
106	RCL 08
107	−
108	÷
109	LN
110	RCL 12	Compute second half of denominator (which is also the numerator)
111	RCL 07
112	−
113	RCL 11
114	RCL 07
115	−
116	÷
117	LN
118	+	Combine two halves, leaving numerator in LSTx
119	RTN
120♦	LBL A	Store or compute f
121	FS?C 22
122	GTO 00
123	XEQ 07	Get denominator (also used for computing R4 and duty cycle)
124	RCL 04	Multiply by R4 and C1
125	×
126	RCL 13
127	×
128	1/x
129♦	LBL 00	Store entered or computed f
130	STO 00
131	RTN
132♦	LBL C	Store or compute R2
133	FS?C 22
134	GTO 02
135	XEQ 05	Compute numerator of R2
136	RCL 06	Compute denominator of R2
137	XEQ 06
138	÷
139	STO 02	Store computed R2
140	RTN
141♦	LBL 02	Store R2 and invalidate VPL and VPH
142	STO 02
143	SF 01	Must recompute VPL and VPH for user-defined R2
144	RTN
145♦	LBL D	Store or compute R3
146	FS?C 22
147	GTO 03
148	XEQ 05	Compute numerator of R3 (same as R2)
149	RCL 06	Compute denominator of R3
150	RCL 05
151	−
152	÷
153	RCL 11
154	RCL 12
155	−
156	÷
157	STO 03	Store computed R3
158	RTN
159♦	LBL 03	Store R3 and invalidate VPLh and VPH
160	STO 03
161	SF 01	Must recompute VPL and VPH for user-defined R3
162	RTN
163♦	LBL E	Store or compute R4
164	FS?C 22
165	GTO 04
166	XEQ 07	Get denominator (also used for computing f or duty cycle)
167	RCL 00
168	×
169	RCL 13
170	×
171	1/x
172♦	LBL 04	Store entered or computed R4
173	STO 04
174	RTN
175♦	LBL 05	Compute numerator common to R2 and R3
176	XEQ 01	Recompute VPL and VPH if necessary
177	RCL 05
178	XEQ 06
179	RCL 01
180	×
181	CHS
182	RTN
183♦	LBL 06	Compute (VOL – VPL – VOH + VPH) * X + VOH * VPL – VPH * VOL
184	RCL 07
185	RCL 11
186	−
187	RCL 08
188	−
189	RCL 12
190	+
191	×	Multiply (VOL – VPL – VOH + VPH) by VPOS or VNEG (now in Y)
192	RCL 08
193	RCL 11
194	×
195	+
196	RCL 12
197	RCL 07
198	×
199	−
200	RTN

Registers and Flags

Register	Use
00	Frequency (Hz)
01,02,03,04	Resistors R1, R2, R3, and R4 (Ohms)
05,06	VNEG and VPOS (Volts)
07,08	VOL and VOH (Volts)
11,12	VPL and VPH (Volts)
13	Capacitor C1 (Farads)
09,14,15,10	Temporary registers

Flag	Meaning
01	VPL and VPH need to be recomputed
22	User supplied input

Revision History

2009-May-25 — Initial release of HP-41C/CV/CX version.

2009-Jun-11 — Fixed a bug where the data entry flag sometimes wasn’t cleared even though there had been no data entry.

2015-Jun-23 — Fixed a bug in the subroutine for computing the denominator of the duty cycle, wherein V_PL and V_PH were accidentally interchanged. Bug was in web-site listing only, not in original program.

                    

Related Articles

If you've found this article useful, you may also be interested in:

• Op-Amp Gain and Offset Design with the HP-41C Programmable Calculator
• Low-Sensitivity Sallen-Key Filter Design with the HP-41C Programmable Calculator
• Low-Sensitivity Sallen-Key Filter Design with the HP-67 Programmable Calculator
• Op-Amp Gain and Offset Design with the HP-67 Programmable Calculator
• Op-Amp Oscillator Design with the HP-67 Programmable Calculator
• Resistor Network Solver for the HP-67 Programmable Calculator
• A Matrix Multi-Tool for the HP 35s Programmable Calculator
• Curve Fitting for the HP 35s Programmable Calculator